Conformal Generative Modeling on Triangulated Surfaces
Victor Dorobantu, Charlotte Borcherds, and Yisong Yue
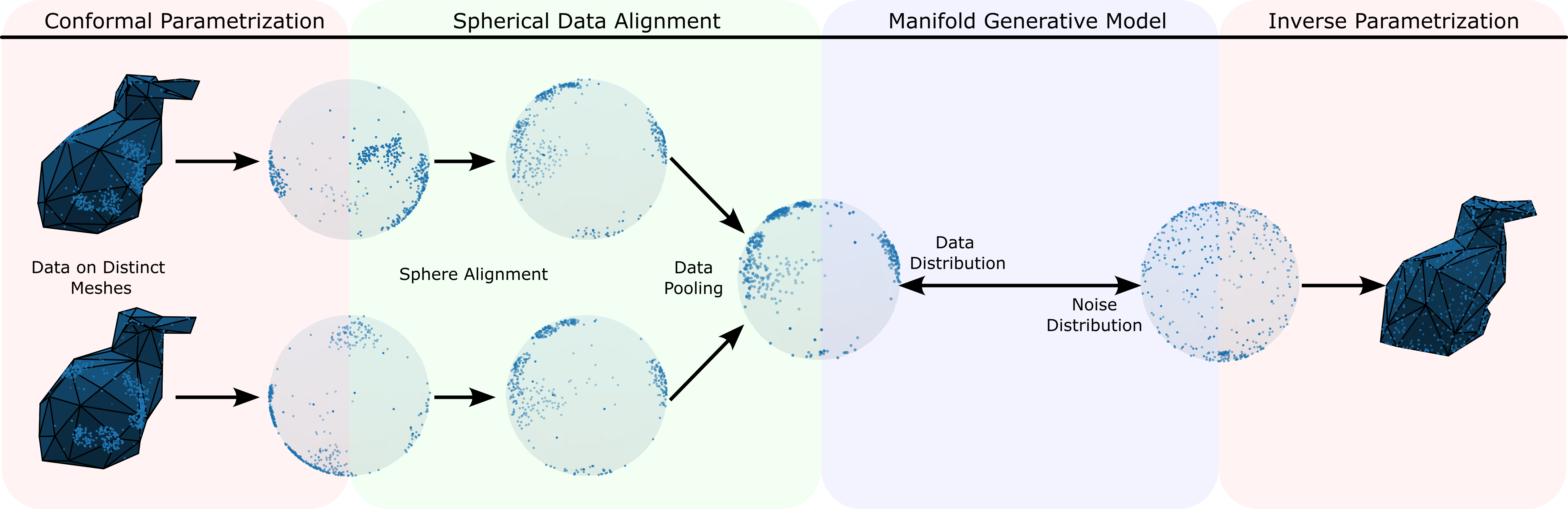
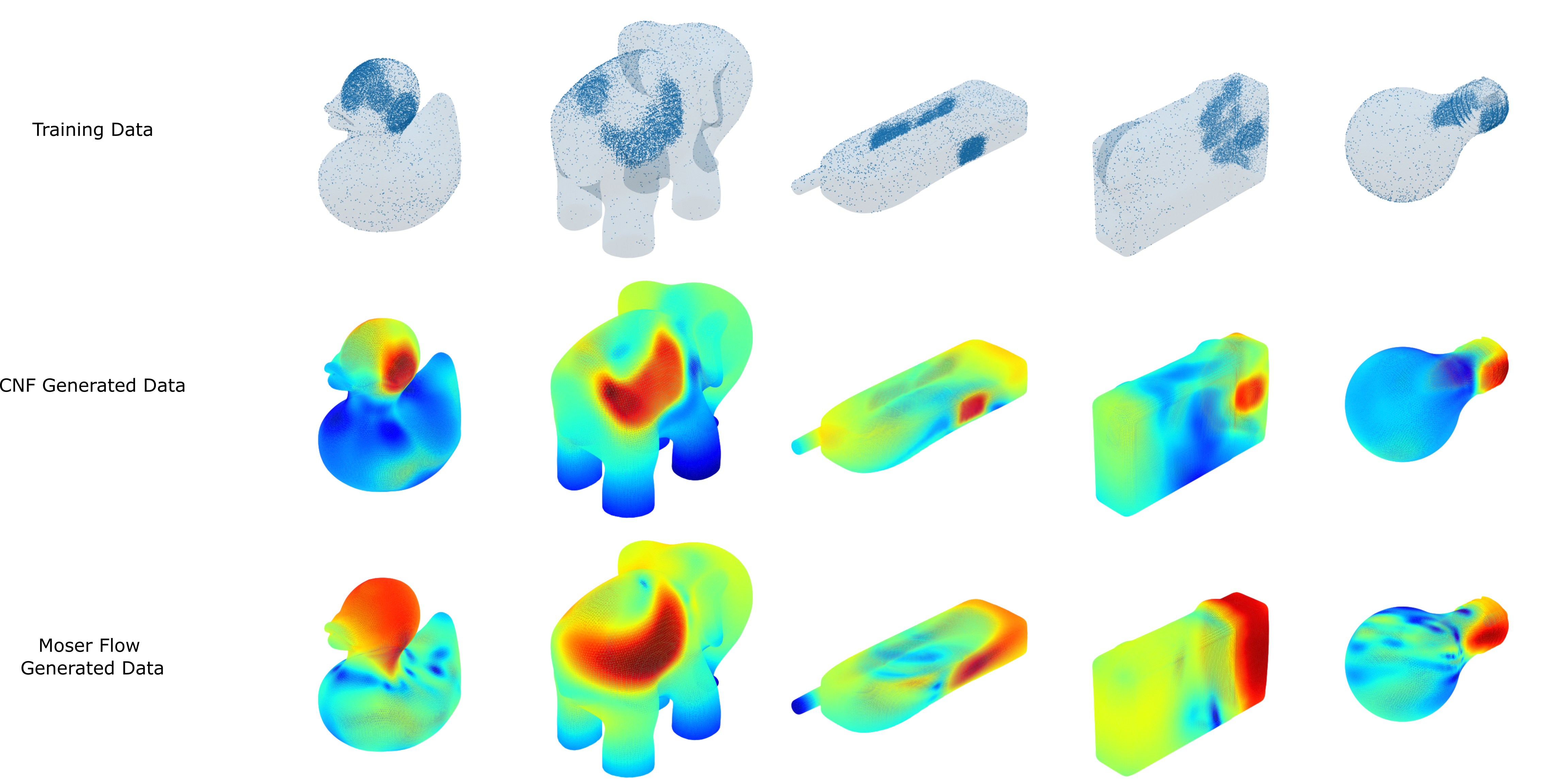We propose conformal generative modeling, a framework for generative modeling on 2D surfaces approximated by discrete triangle meshes. Our approach leverages advances in discrete conformal geometry to develop a map from a source triangle mesh to a target triangle mesh of a simple manifold such as a sphere. After accounting for errors due to the mesh discretization, we can use any generative modeling approach developed for simple manifolds as a plug-and-play subroutine. We demonstrate our framework on multiple complicated manifolds and multiple generative modeling subroutines, where we show that our approach can learn good estimates of distributions on meshes from samples, and can also learn simultaneously from multiple distinct meshes of the same underlying manifold.